Chapter 3. Graphical User Interface
Prev   Next

Chapter 3. Graphical User Interface

Table of Contents

1. Menus
2. Toolbar
3. Graph Editor
Property
Element
Hierarchy
4. View Editor
5. Standard views
Node Link Diagram view
Table view

We suggest to run Tulip and experiment with the concepts explained while reading this Manual. Here are the components of the main window:

1. Menus

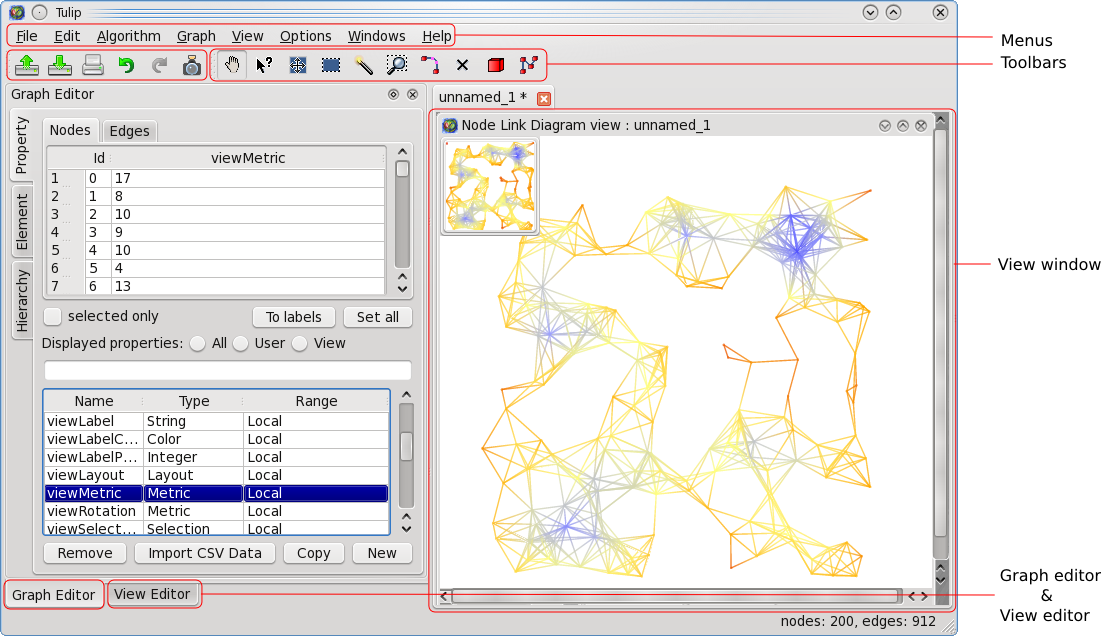
  • File: usual file operations (New, Open, Save, Save as, Close Tab, Exit) and

    • Import: when import plugins are installed, they go into this menu.

      • File: import graphs in various file formats, such as Adjacency Matrix (see Wikipedia: Adjacency Matrix for details), GML (used by the graphlet system, a toolkit for graph editors and graph algorithms), dot (graphviz), or TLP (Tulip's own file format).

      • Graph: plugins to generate graphs (random or deterministic):

        • Complete General Graph: complete graph

        • Complete Tree

        • Grid: 2D grid

        • Grid approximation: This algorithm creates the specified number of nodes and places them randomly in the 2D plane. Then it adds an edge between all pairs of nodes that are at distance at most d. d is adjusted so that the average degree is approximately the degree requested.

        • Random General Graph

        • Random Simple Graph

        • Uniform Random Binary Tree

      • Misc: plugins to capture the tree structure of a file system directory under a selected root, or crawl the graph structure of a web site.

    • Export. save a graph in GML or TLP formats. Plugins can be installed to support more file formats.

  • Edit:

    • Cut

    • Copy

    • Paste. Note that a copied element is placed at the location of the original; use right-click View → Center View or Ctrl+Shift+C if the pasted element is outside of the screen

    • Find . This tool has 4 options:

      • Replace: Replace the current selection (nodes or edges already selected).

      • Add: Add the nodes (or edges) to be selected to the current selection.

      • Remove: Remove nodes (or edges) from the current selection.

      • Intersect: Select the intersection between the nodes (or edges) TO BE selected, and the ones from the current selection.

    • Select All ,

    • Delete selection: delete selected nodes and edges,

    • Deselect all ,

    • Invert Selection .

    This menu also contains Create group, Create subgraph, Undo, Redo.

  • Algorithm:

    • Selection: select nodes and/or edges based on advanced criteria. (Selecting means assigning the 'viewSelection' property, see Section 2, “Graph properties” for details). For example, the 'Loop Selection' algorithm detects all edges for which the starting and ending nodes are the same.

    • Color: computes the color (the 'viewColor' property, see Section 2, “Graph properties” for details) of the graph elements. A default one, 'Metric Mapping', is provided; it allows to color all graph elements according to a metric property.

    • Measure: compute and assign a value to the 'viewMetric' property of graph elements, see Section 2, “Graph properties” for details. For example, when running the 'Degree' algorithm, the degree (the number of neighbors) is computed and stored, for each node, into its 'viewMetric' property.

    • Layout: compute the position of each node. For example, the 'Circular' algorithm places all nodes along a circle.

      Before:

      After:

    • Size: compute a size (the 'viewSize' property see Section 2, “Graph properties” for details) of the graph elements.

    • General: more general algorithms: subgraphs, quotient graphs, groups... For example the 'Equal Value' algorithm create subgraphs for which the elements have a chosen value for a chosen 'metric' property.

    For more information, see Section 1, “Algorithms”.

  • Graph :

    • Tests: test if the graph obey some constraints:

      • Simple : Is the Graph Simple? As opposed to a multigraph, a simple graph is an undirected graph that has no loops and no more than one edge between any two different vertices. For more information, please visit: Wikipedia: Simple graphs

      • Directed Tree : A directed tree is a directed graph which would be a tree if the directions on the edges were ignored. Some authors restrict the term to the case where all edges are directed towards a particular vertex, or all away from a particular vertex. More information: Wikipedia: Directed Tree

      • Free Tree: A tree without any designated root is called a free tree. More information: Wikipedia: Free tree

      • Acyclic: A graph is acyclic iff it contains no cycle. (A cycle is a path having the same start and and nodes.) More information: Wikipedia: Acyclic graphs

      • Connected: A graph is connected iff there is path path from any node to any other node. More information:

        Wikipedia: Connectivity

      • Bi-connected : A connected graph is biconnected if the removal of any single node (and its adjacent edges) does not disconnect the graph. More information:Wikipedia: Biconnected Graphs

      • Tri-connected : If it is always possible to establish a path from any node to an other one even after removing any 2 nodes, then the graph is said to be tri-connected. More information: Wikipedia: k-connected graphs

      • Planar : A graph is said to be planar if it can be drawn on the (Euclidean) plane without any edges crossing. More information: Wikipedia: Planar Graphs

      • Outer Planar : A graph is said to be outer planar if it has an embedding in the plane such that its nodes lie on a fixed circle and its edges lie inside the disk without any crossing. More information: Wikipedia: Outerplanar Graphs

    • Modify : Modify the whole structure of a graph, to ensure the graph has one of the above properties:

      • Make Simple : Makes the graph simple (by removing self loops and parallel edges, if any). see Algorithm documentation

      • Make Acyclic Makes the graph acyclic (by replacing each loop with a triangle, then reversing some edges).

      • Make Connected If the graph is not connected, adds edges to make the graph connected.

      • Make Bi-connected If the graph is not biconnected, adds edges to make the graph biconnected.

      • Make directed : If the graph is a free tree, make it directed. If only one node is selected, this one will be considered as the root node. If none is selected, Tulip will heuristically choose the center of the graph as the root node. More information: Wikipedia: Directed Tree

      • Reverse selected edges: Exchange source and target of those edges.

  • View: click one and a new subwindow will be created in the view window. For instance, table view displays the list of nodes and the list of edges. See Section 5, “Standard views”.

  • Windows: manages the subwindows of the view window.

  • Options: enable/disable the display options, and show the Graph or View editor:

    • Display options:

      • Force ratio: Tries to keep a good Height/Width ratio for the graph layout.

      • Map metric: Whenever a measure algorithm is run, show its result by updating the graph colors (i.e. applies the Color / Metric Mapping algorithm)

      • Morphing: when a new layout is applied, displays an animation morphing the old layout to the new one.

    • Show Graph/View editor: if you have closed the Graph or View editor tab (in the left dock widget), you can show it again thanks to this menu

  • Help: Documentation (the present one), Preferences, Plugins manager, About this software, including version number.

Prev   Next
Chapter 2. Tutorial Home 2. Toolbar