Before anything, download, and open this tulip graph file. Click on the tab Hierarchy (in the info editor window) and select the subgraph GRCite. You need to delete the other sub graphs by doing a right click on there name, and then "remove".
This graph represent the relations between authors, conferences and papers. To distinguish paper, conferences and authors, we will re-color them :
Select all papers : Press on Ctrl+F to display the find tool. In the Input Property field, select the property "type". And on the line below, set the filter function to "=" and the filter value to 0, before clicking on the Find button.
Re-color the nodes in red : Select the tab Property (in the info editor). Check the "selected only" option. Select the property viewColor, and, by clicking on the button "Set all" choose the red color.
Repeat the actions above, for authors (type = 2 ) and conferences (type = 1) with other color (blue , yellow).
You should obtain something like this :

Select an author :
Let's pick a single author to investigate, in this case George Robertson. First, we interactively select that node by hitting Ctrl+F for the find tool, choosing the "titleshort" property, the "=" as filter fuction, and the regular expression "G.*Rob.*" as filter value. We then quickly check to see how he is connected to the entire graph by temporarily moving that node away from the others to see roughly how many edges are attached to it.
Following is what you should get :

Go deeper :
We then select the menu item Algorithm->Selection->Reachable Sub-Graph, type 1 for the distance into the popup panel and 0 for the direction of the edges (outgoing). We then select the menu item Edit->Create Subgraph to save this selection for further manipulation, naming it GR.1hop.outgoing. We then select this new subgraph in the hierarchy tab, and lay out this subgraph using a hierarchical drawing algorithm (Algorithm->Layout->Hierarchical->Hierarchical graph).
We can see simply from the drawing which papers were published first, as they are cited by the later ones. Robertson has published 11 papers in this database. The coloring by the number of citations (Algorithm->Color->Metric Mapping, with field property set to "arityOut" ) shows that "Cone Trees" is his most influential work.
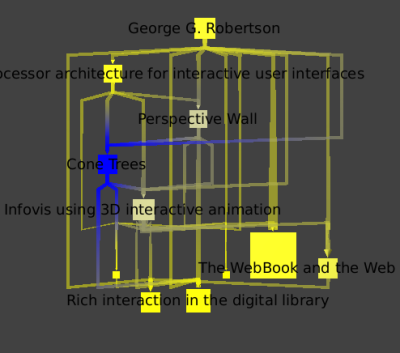
Finally, we select all papers by hitting Ctrl+F for the find tool, choosing the type property, the "=" filter, and the value 0 for papers. We explicitly add Robertson to the selection using the selection tool to select its edges too (see below), and save this whole set to a new subgraph that we name GRCitesub:

In the new subgraph, we then select the Robertson node. Again as above, use the Algorithm->Selection->Reachable Sub-Graph algorithm, pick a depth of 2 to find all papers that cite a paper written by Robertson, and save the resulting subgraph using the Edit->Create Subgraph menu. The final image shows the result of using the Algorithm->Layout->Hierarchical Graph layout.

You can now close this graph since we are going to use an other one for the following of this tutorial. The next graph is similar to the this one but, has coauthorship edges linking authors who write papers together. You can download it and open it in tulip.
Here we focus on the relationship between two authors, in this case Robertson and Card.
To select them use the find tool, with, at the first time the regular expressions : "G.*Rob.*". And at a second time, the regular expression ".*Card.*" and the "add" option checked. To move those selected nodes away from the main layout, use the "moving selection" tool. If you click on one of the node, you will be able to move both nodes at the same time.

Select Card and Roberts at the same time ( Press Shift while clicking on a node). Select all their neighbors by applying the Algorithm->Selection->Reachable Sub-Graph algorithm with distance 1. Create a new Subgraph.
Following is a hierarchical layout of the neighborhood of all outgoing edges one hop away; that is, the publications and coauthors of the union of Card and Robertson.

You can repeat those operations for Robertson only and Card only :

The similarity of these final three images shows the very strong ties between these two authors.
You can now close this graph since we are going to use an other one for the following of this tutorial. The next graph is similar to the old one but, has links between author and conference by following links from author to paper, and from paper to conference. Then, delete papers. You can download it and open it in tulip.
To show the large-scale structure of this dataset, we colored Authors in green and conferences in blue with a GEM layout (Algorithm->Layout->Force Directed->GEM). We deleted all the papers nodes.

By zooming in :
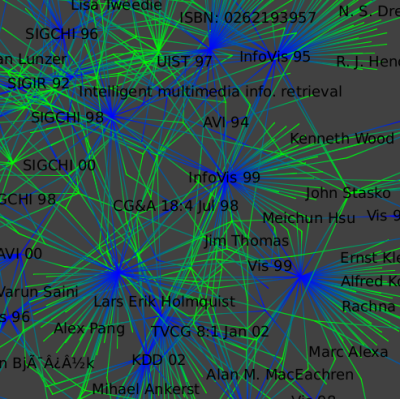
We select only the large connected component (the big set of nodes) : Select a fiew nodes in the center of the component and run the "Reachable Subgraph" selection algorithm with distance set to 50.
Color the authors by the Strahler metric: Run the Algorithm->Measure->Graph->Strahler algorithm and then a Algorithm->Color->Metric Mapping algorithm.
Finally, we color papers in white.
This layout, shows the branching structure of the dataset.

To distinguish authors and conferences :
Select all authors (nodes of type 2) and set their viewLabelColor property to red.

It is very simple to see top conferences since they are the ones where the number of authors is high. The Metric Degree will help us to highlight them (Algorithm->Measure->Graph->Degree ).
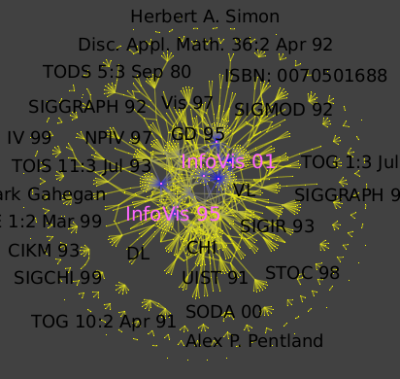
Run the Algorithm->Measure->Graph->Strahler algorithm to see strong ties between conferences and authors :

Then run the Algorithm->General->Convolution, the value of the "discretization" parameter should be near 30 to obtain 5 clusters ) (Picture 1) to obtain the following clusters (Picture 2):


The Strahler-Convolution clustering yields five clusters, according to increasing centrality. The first cluster is mostly yellow, and contains most of the data. The second cluster contains a next tier of 26 authors that have had a relatively strong impact. The third cluster contains a group of 7 influential authors (Chi, Bederson, Eick, Rao, Pirolli, Ward, and Brown), and the fourth cluster (Roth, Robertson, Keim, and Stasko) is yet more central. The fifth cluster is the single node of Mackinlay, and the last one is Card and Shneiderman. Our automatic clustering method clearly yields very believeable results in this case.
In the last section, we will use an other graph. Please download it and open it in tulip.
To be able to see the labels within metanode check the "metanode label" visible box in the Layers tab in Rendering Parameters dialog.
The clusters have been computed using the Algorithm->General->Strength clustering algorithm.
The overview image from the previous section, showing the graph of all authors and papers, is extremely cluttered. In the previous task we show one way to extricate more information, by finding the most important items via convolution clustering. Another clustering approach, small-worlds clustering, allows us to instead navigate through a hierarchical subdivision of the entire dataset. The simplified overview allows us to understand the graph's high level structure. The strength metric computes the number of cycles of length 3 and 4 passing through each edge, normalized by the maximum possible value. The first image shows the clustered dataset. Small-world navigation is useful when exploring an unfamiliar graph to quickly find the structure of complex components. The eccentricity metric (Algorithm->Measure->Graph->Eccentricity), which measures whether nodes are peripheral (here in yellow) or central (here in blue), guides us to complexity immediately. This metric is O(n^3), but the small-world decomposition simplifies the graph, making the computation tractable.

The picture shows zooming in towards the node that has many blue lines leading to it.
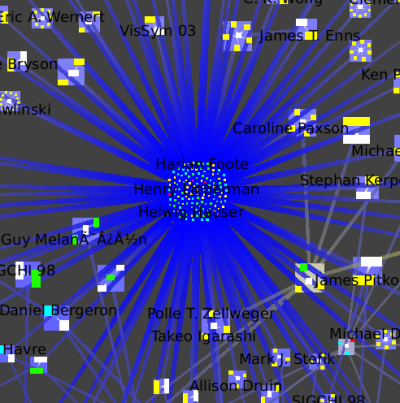
We then jump inside that cluster (Select the metanode, Right Click, Go inside), which is itself a small-world graph.

We once again zoom towards the most central node with many blue edges, where we see a cluster that has the InfoVis 96 conference and all the authors who only published the infovis community in that year.


We see this star shape small-world decomposition only for the InfoVis symposia, because of the nature of this dataset: it is only the InfoVis symposia that have a complete set of authors and papers available.