Each graph can be modified with algorithms for the layout, the set of selected elements, the size of nodes, the value attributed to an element (node or edge) named metric, the colors. An other advantage of Tulip is that it is easy to add a new algorithm in the structure; this way, it is able to include lot of algorithms. As explain in the Section 1, “Main window : Menus”, the algorithms are accessed by the Algorithm menu. Several categories are in there : Selection, Color, Layout, Measure, Size, General. They modify the properties of the graph elements.
The induced Sub-Graph algorithm can be used to obtain the edges that are between selected nodes.
Here is an example :
Before :
After :

The Algorithm of Kruskal is used to create a minimum spanning tree out of a connected graph.
It is divided in several steps :
Make a list of the edges starting with the "shortest" one, ending with the "longest one".
Add all edges with their from/to nodes to the tree as long as you don't have any cycle.
Let's take an example : We have a set of airports, Bordeaux, Paris, L.A ..., the nodes, and a set of Airports connections, the edges.
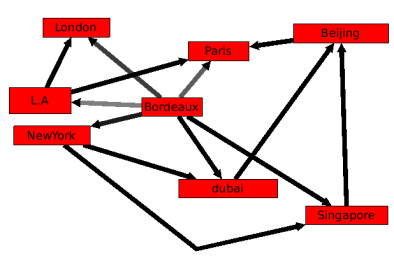
As you can see, this makes a very complicated Graph. As edges do not all have the same weight (in terms of price, distance, ...), some of them are not really important (the ones with a high weight). The algorithm of kruskal will select the ones that we can't remove.
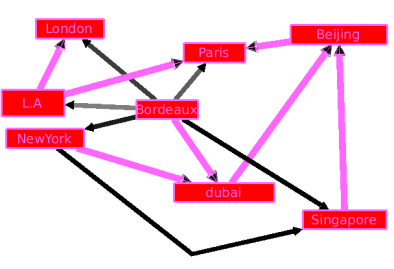
By creating a sub-graph we get a simple graph which is much more easy to read.
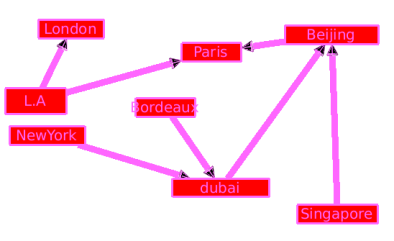
Please visit Wikipedia : Kruskal's algorithm for more details.
This selection algorithm is able to select the loops of a graph. A loop is an edge that has the same source and target.
This selection algorithm highlights the multiple-edges also named parallel-edges in a graph.
Two edges are parallel only if they both have the same target and same source.
This selection algorithm enables to find all nodes and edges at a fixed distance of a set of nodes. It takes three parameters :
Distance: number of edges to follow.Direction: 0 means directed, 1 reverse directed, 2 undirectedStarting nodes: the selected nodes of this selection property ( boolean ) will be used as starting nodes.
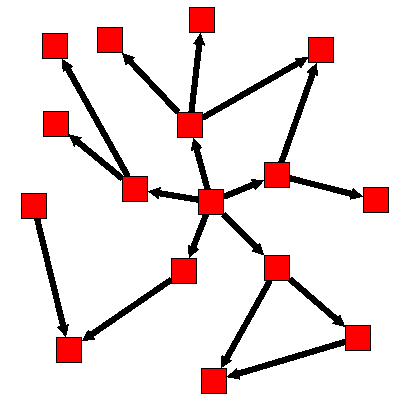
In the following example, 'distance' equals to 1, 'direction' equals 0, and the starting node is the one in the center.
Before :
After :
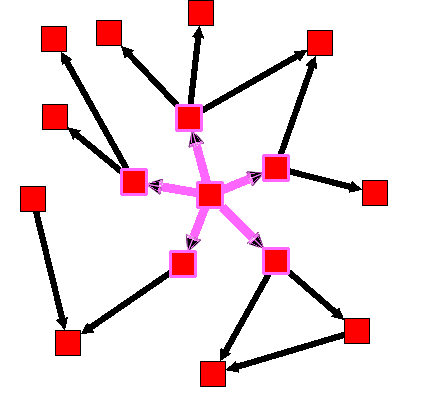
This selection algorithm can be used to select a sub-graph without any cycle.
This algorithm can be used to create a set of spanning trees out of the graph.
A tree is a special kind of graph that has the following properties :
Has a root (a starting point node).
A node have severals sons and their is only one edges targeting each sons.
Doesn't have any cycle.
A leaf is an "ending node".
The metric mapping algorithm can be used to re-color the nodes of the graph after using a measure ( the section called “Measure” ) algorithm.
This Algorithm takes 5 parameters :
Property: Property is a metric value. It is used to affect scalar values to graph items.Colormodel: Color can be either 1 or 0. 1 for RGB interpolation and 0 for HSV interpolation.Type: If type is checked, the color mapping will be uniform, which means that if you have 2 nodes with the property value equals to 0, there will be 2 nodes colored in "color1" .If type is not checked, the color quantification will be linear, which means that if you have 2 nodes with the property value equals to 0, there will be 1 node colored in "color1" and an other with a lighter color1.
Color1: Color1 will be the color of the node that has the lowest value (according to the Property field)Color2: Color2 will be the color of the node that has the highest value (according to the Property field)
Let's take an example :
As you can see here is a graph where no metric values has been computed.
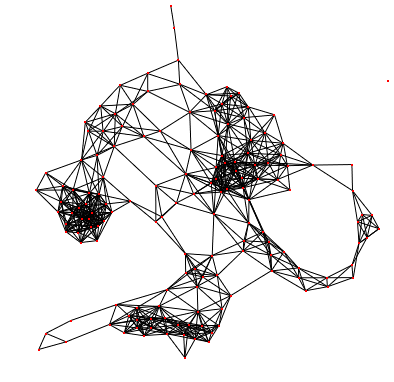
After applying the degree algorithm, the graph gets colors !

If you do not have any colors (on edges), see if you have checked the "Color interpolation" in the rendering parameters window ( CTRL+R) . After applying the "Metric mapping" algorithm ("type" checked, "colormodel" equaled to 1 , "Color1", a kind of red and "Color2" a kind of green ) we will obtain the following graph.
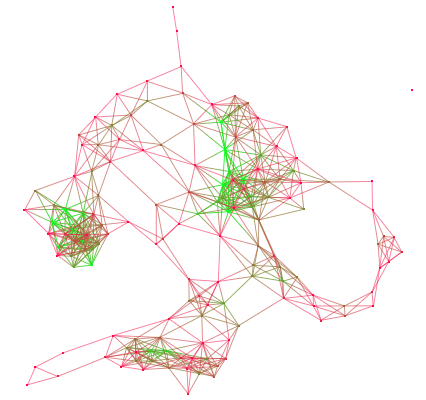
Measure algorithms are used to compute different metrics (on edges or nodes). The computed values are assigned to the viewMetric property.
Betweenness is a centrality measure of a node within a graph. Nodes that occur on many shortest paths between other nodes, have higher betweenness metric than those that do not. As this algorithm will compute a global measure, it can take a long time to finish. See Widipedia : Betweenness for more details.
This algorithm can only be used on simple graphs (graphs with no loops).
The cluster algorithm is a measure algorithm that can determine whether or not a graph is a "small-world network". The clustering measure is a local measure that gives the connections rate of a node and its neighbors.
Let's take an example :
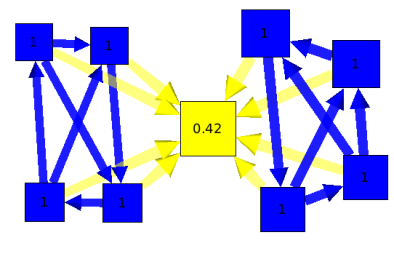
On this graph, and by looking at the clustering measure, you can see 2 "communities" (nodes in blue) and a hub (node in yellow).the hub is the only way to connect the two communities.
For more details, please visit http://en.wikipedia.org/wiki/Clustering_coefficient.
This algorithm will save the degree of each node in its viewMetric property. It takes two parameters :
Type : Is the type of degree you want to compute. In : Edges that comes onto the node. Out : Edges that are going away from the node. InOut : Using both (in and out).
Metric : This parameter can take all double properties, but by default it will take : None, 'viewBorderWidth', 'viewMetric' and 'viewRotation'. If you choose none, the degree of the node will be the sum of the edges. If you choose the 'viewMetric' value, degree of the node will be the sum of edges wiewMetric property. As of viewBorderWidth and viewRotation.
This plug in compute the eccentricity of each node, eccentricity is the maximum distance to go from a node to all others. In this version the value is normalized (1 means that a node is in the center of the network, 0 means that a node is the more eccentric in the network). The eccentricity will be saved in the viewMetric property of each node.
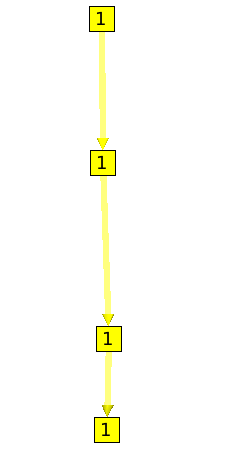
The Strahler algorithm is very powerful. It can for example point out important path in a graph, by computing for each node the degree of ramification of its (spanning) sub-tree. Following is a graph with only one path. You can see that each node have the same Strahler number (1).
But on this graph, more the degree of ramification is important and more the number of strahler will be high.
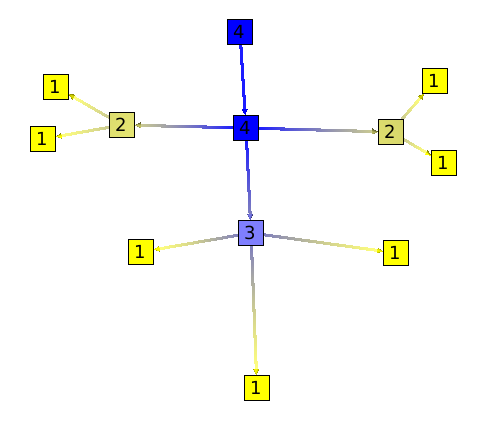
Note that this graph could represent anything, a program (inclusion of sources files), or a city road traffic.
Parameters :
All nodes :If not checked, the algorithm will choose a node (a source node) and will apply the algorithm to this node only. If checked, the algorithm will be applied to all nodes.Type :This parameter can take 3 different values : Register which will force the algorithm to give an indication on the degree of ramification (for trees), Stack, that will force the algorithm to give an indication on the number of nested cycles (for graphs), and at last, All, that will ask the algorithm to use both registers and stack.
For more information please visit http://en.wikipedia.org/wiki/Strahler_Stream_Order
Graph must be simple (no loops).
This algorithm will compute the strength of edges. Every edges with small values are important in the way that their removal can disconnect two connected components. Every edges with a high value metric may belong to a strongly connected component.
A connected graph is biconnected if the removal of any single node and its edges can not disconnect the graph. The biconnected components of a graph are the maximal subsets of nodes such that the removal of a node from a particular component will not disconnect the component. Note that unlike connected components, a node can belong to multiple biconnected components. For example we can use this algorithm on an airlines graph. Such as the one following.
The result is, 3 biconnected components :
1 : Paris, New York, L.A, Madrid.
2 : Paris, Berlin.
3 : Berlin, Moscow, Prague.
The intersection of those 3 biconnected components is Berlin and Paris. Which means that Berlin and Paris are two articulation points of our graph.
A connected component is a maximal connected subgraph. Two nodes are in the same connected component if and only if there exists a path between them.
After running the algorithm, the index of the connected component of a node is saved in its viewMetric property. It is the same for the edges.
For more details please visit : Wikipedia:Connected Component Algorithm documentation
The connected tree component algorithm can be useful to find parts of a graph that are trees. Here is an example :
Following is a graph with on the left side, a tree. This graph forms a unique connected component.
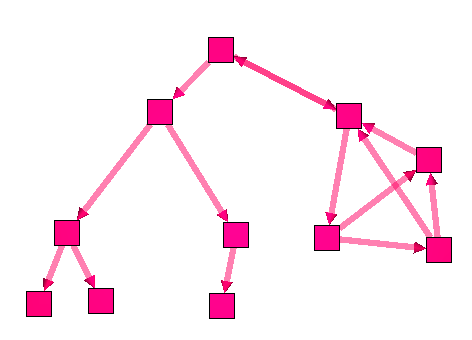
As you can see, the algorithm divided the graph into 2 components.
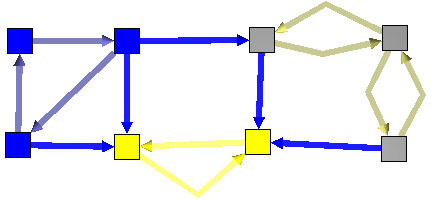
A directed graph is said to be strongly connected if for every pair of nodes S1 and S2, it exists two edges e1 and e2 such as :
The Source of e1 is S1 and Target is S2 .
The Source of e2 is S2 and Target is S1.
The strongly connected components of a directed graph are its maximal strongly connected subgraphs.
These form a partition of the graph. Here is an example :
Before :
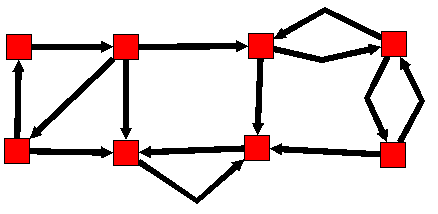
After :
To use the following algorithms the graph has to be acyclic. A graph is acyclic if it contains no cycle.
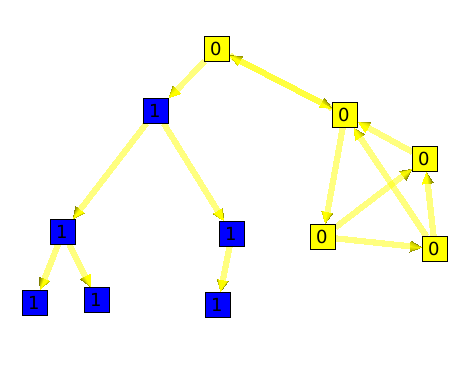
The dag level algorithm will compute the depth of each node, as on the following example :
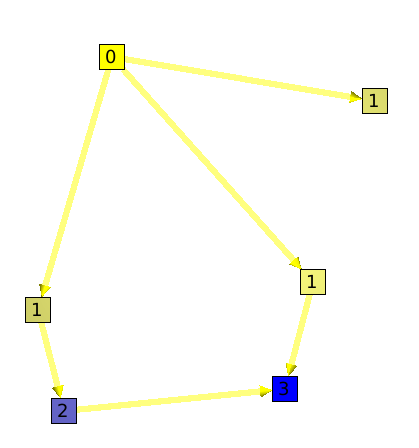
The depth algorithm will compute for each node, the maximum number of edges to follow to find a leaf.
The leaf algorithm will compute for each node its number of leaves.
Here is an example :
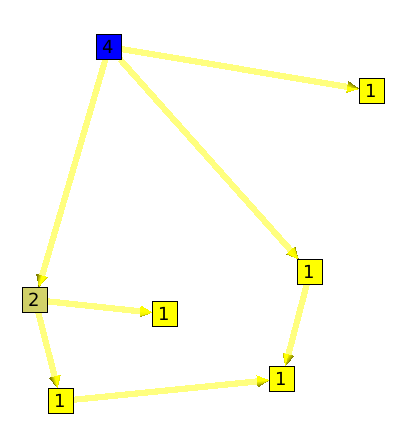
The Node algorithm, will sum for each node the number of its children nodes plus him self. Algorithm documentation
This algorithm will count for each node the number of paths that goes through it.
Here is an example :
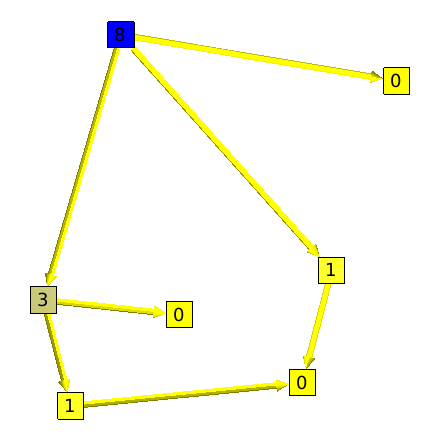
A segment, is a set of nodes that are all on one and only path. The graph showed on the left side of the example is a segment.
The segment algorithm will count, for all nodes, its number of edges without ramification.
Following are two graphs. On the left one you can see that the root "has" 3 edges without ramification. But, on the right graph all nodes (without considering leaves) have only 1 edge without ramification.
This algorithm can be useful to see how the graph is formed. Indeed, if the root has a small value, it will mean that the graph has a "good" ramification. But if the root has a high value, it will mean that the graph a lot of segments.
Compute the maximum outdegree of the nodes in the subtree induced by each node. To access to the degree of a node it is recommended to use directly the degree function available in each Graph. Algorithm documentation
The "id" algorithm will, for each node and edge, save their id number in their viewMetric Property. For example, if we have a node called Node 9, its id number will be 9. Algorithm documentation
Random will just save a random number (from 0 to 1) in the viewMetric property of each node and edges Algorithm documentation
Warning ! : Some of the following algorithm have no effect if the option "Force Ratio" is checked.
This algorithm can only be applied to 3-connected graphs. A graph G is said to be 3-connected if there does not exist a set of 2 nodes whose removal disconnects the graph. (Triangle Layout) Algorithm documentation
Create a planar sub-graph with polylines with a good angular resolution which will make the graph clear and easy to read. Algorithm documentation
To represent a tree, a hierarchical layout is the easiest way to understand the tree structure. But this layout has a big weakness when the tree has a lot of nodes : it does not effectively use the space where the tree is displayed. That is why we need different layouts.
The Bubble Tree algorithm can be use to change the layout of a tree. On the new layout, a node will be on the center of a circle, and its children will be on the circle. This new layout has the following properties :
The edges should not cross each other.
The polyline used to draw an edge should have the least possible bends.
The minimal angle between two adjacent edges of a node n should be nearest to 2pi / deg (n). This property will improve the angular resolution.
The order of children of a node should be respected in the final drawing.
Here is an example :
The following graph has the default layout (hierarchical layout). It has a pretty bad angular resolution. Indeed, we do not see the leaves, but only a large black rectangle of edges.
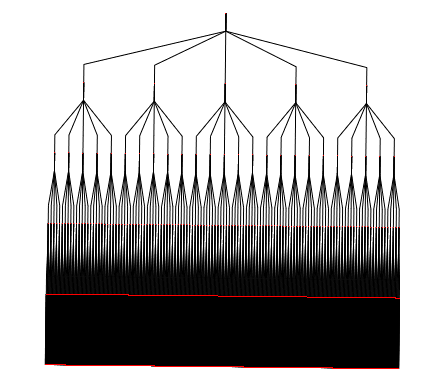
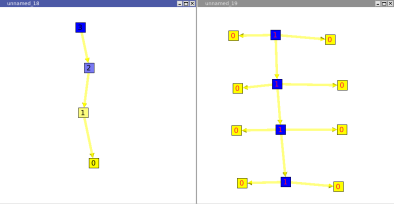
Here is the same tree with a Bubble Tree layout. The angular resolution is much better.
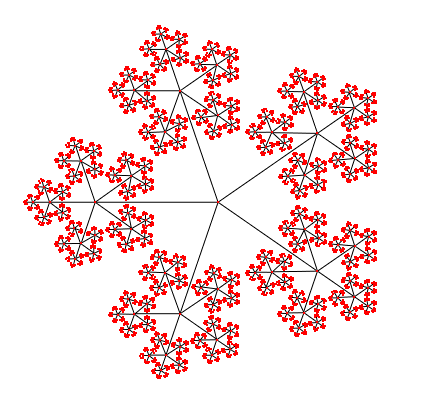
The cone tree is a 3d layout which seen from the top, looks like a bubble tree. It takes two parameters:
node size : size of the node will depend of the metric that you choose. The Algorithm will consider that parameter so that no nodes overlap themselves. This can be useful, if you want a node to be far from the others, just take a new size Metric and give a higher value to that specific node.
Orientation : Vertical / Horizontal
Here is an example of this layout. On the left side you can see a tree with a hierarchical (classic) layout, and, on the right side, the same tree, but with a cone tree layout.

The dendrogram layout is a hierarchical layout on which every leaves are displayed on the same layer.
A dendrogram is a tree diagram frequently used to illustrate the arrangement of the clusters produced by a clustering algorithm. Dendrograms are often used in computational biology to illustrate the clustering of genes.
The algorithm takes 4 parameters :
node size : size of the node will depend of the metric that you choose. The Algorithm will consider that parameter so that no nodes overlap themselves. This can be useful, if you want a node to be far from the others, just take a new size Metric and give a higher value to that specific node.
orientation : up to down, left to right, right to left or down to up.
layer spacing : space between the levels of the Tree.
node spacing : space between sibling nodes.
The hierarchical tree layout looks the same that the dendrogram layout or the improved walker layout but takes an other parameter, "edge length".
node size : size of the node will depend of the metric that you choose. The Algorithm will consider this parameter so that no nodes overlap themselves. This can be useful, if you want a node to be far from the others, just take a new size Metric and give a higher value to that specific node.
edge length : this parameter can take a property of type int, and will be used to place a node on a specific layer. If its value is 1, no thing will happen, but if its value is 2, the node will be placed on the next layer.
orientation : vertical/horizontal;
orthogonal : enables the drawing of the edges, orthogonally bent.
layer spacing : space between the levels of the Tree.
node spacing : space between nodes sibling nodes.
bounding circle : if checked, the estimation of overlapping nodes will be computed with bounding circles instead of bounding rectangles.
The improved walker layout is just a hierarchical layout. Algorithm documentation
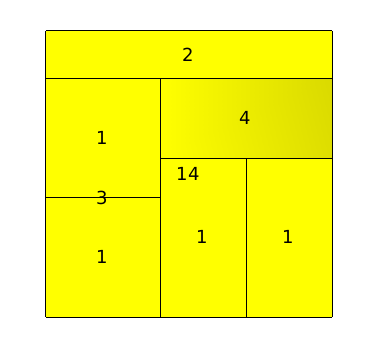
The squarified tree map layout, will place nodes in nested rectangles. For example, lets take a tree with a root and two sons, the layout will draw a rectangle for the root containing two other rectangles (its sons). This layout can be very useful for analyzing disks usages.
Here is an example :
Following is the tree a a file system containing 6 file of 1Mb, and severals directories.
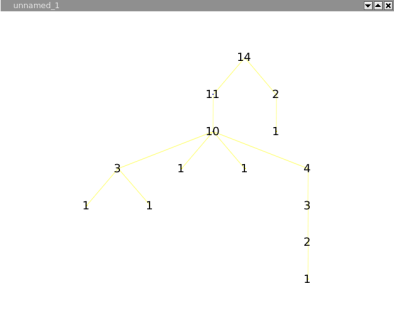
The same graph, with a squarified tree map layout :
Using the 3D, we can see how the layout is done :

This layout looks like the improved walker, but does not pack the nodes. The result is a nice hierarchical tree in which nodes does not overlap. Algorithm documentation
This layout, is the same as the squarified tree map layout, but the squarified tree map uses shadows to draw the tree. Algorithm documentation
On this layout, nodes of the same layer are placed on a circle whose center is the root. Algorithm documentation
On this layout, every nodes are placed on a circle. Algorithm documentation
This layout groups connected components of the graph so that they do not overlap themselves and that lost space is minimized (packing). It takes 4 parameters :
node size : size of the node will depend of the metric that you choose. The Algorithm will consider that parameter so that no nodes overlap themselves. This can be useful, if you want a node to be far from the others, just take a new size Metric and give a higher value to that specific node.
Rotation.
Coordinates.
Complexity.
Here is an example (left = before, right = after)
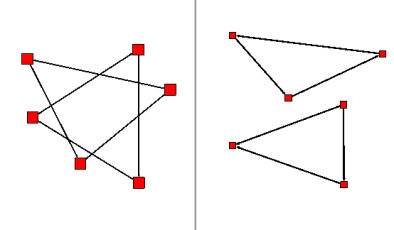
Force Directed layouts will try to place nodes so that, the distance in the graph (metric of the edges) should be the closest to the distance on the drawing.
Warning ! : The previous property is not 100%.
The GEM layout, unlike the HDE layout, works on all graphs. But it can take a very long computing time if the graph has more than 2000 nodes. Algorithm documentation
This layout, will place the nodes of a graph as if the graph was a tree. Algorithm documentation
The auto sizing algorithm will resize nodes and edges of a graph so that the graph gets easy to read. The size of a node will depend on the number of its sons.
Convolution clustering is an approach to partitioning a graph that gives the user interactive control over how many clusters to create. Tulip calculates a density function based on the chosen metric, displays a convolution of its histogram, and partitions the graph according to the humps in the histogram.
This algorithm will create sub-graphs in which all nodes or all edges (not both at the same time), have the same value. The 'Connected' parameter indicates whether the subgraphs have to be connected or not.
This algorithm will divide the graph in 2 different subgraphs; the first one will contain nodes that have the viewMetric value under than a certain limit, and, the other one, in which nodes will have a the viewMetric value higher than the limit. Then, the algorithm will be re-applied to the subgraph (the one with higher viewMetrics) until the subgraph contains less than 10 nodes. Algorithm documentation
This algorithm will create a metagraph. The metanodes will represent the subgraphs that already exist, and a metaedge will be created between two metanodes if and only if it exist an edge whose source is a node of a subgraph, and the target a node of an other subgraph.
Parameters :
oriented : this parameter indicates whether the graph has to be considered as oriented or not. If it is the case, two metaedges may exist between two metanodes One representing the edges from the nodes of subgraph 1 to the nodes of subgraph 2, the second representing the edges from the nodes of subgraph 2 to the nodes of subgraph 1.
node function : this parameter enables to choose the function used to compute a measure value for a meta-node using the values of its underlying nodes.
edge function : this parameter enables to choose the function used to compute a measure value for a meta-edge using the values of its underlying edges.
meta-node label : this parameter enables to choose the string property used to compute the label of the meta-nodes. An arbitrary underlying node is choosen and its associated value for the given property becomes the meta-node label.This parameter enables to choose the string property to use when naming mete-node.
use name of subgraph : this parameter indicates whether the meta-node label has to be the same as the name of the subgraph it represents. When checked, it superseeds the choice of the previous parameter.
recursive : this parameter indicates whether the algorithm has to be applied along the entire hierarchy of subgraphs.
edge cardinality : this parameter indicates whether the cardinality of the underlying edges of the meta-edges has to be computed or not. If yes, the property edgeCardinality will be created for the quotient graph.
The strength clustering algorithm will recursively create subgraphs that are nested "small-worlds".